matematikekseni - Matris )

Matematikte matris veya dizey, dikdörtgen bir sayılar tablosu veya daha genel bir açıklamayla, toplanabilir veya çarpılabilir soyut miktarlar tablosudur. Dizeyler daha çok doğrusal denklemleri tanımlamak, doğrusal dönüşümlerde (lineer transformasyon) çarpanların takibi ve iki parametreye bağlı verilerin kaydedilmesi amacıyla kullanılırlar. Dizeylerin toplanabilir, çıkartılabilir, çarpılabilir, bölünebilir ve ayrıştırılabilir olmaları, doğrusal cebir ve dizey kuramının temel kavramı olmalarını sağlamıştır.

BİLGİLER: Matris (dizey) sayma sayılarını dikdörtgen halinde dizip gösteren bir matematik tablodur. Örneğin:

$mathbf{A} = begin{bmatrix} 12 & 83 & 16 21 & 22 & 17 14 & 9 & 20 16 & 0 & 5 end{bmatrix}.$

Bir diğer notasyona göre dikdörtgen parantezler yerine eğri şekilli parantez kullanılır:

$mathbf{A} = begin{pmatrix} 9 & 8 & 6 1 & 2 & 7 4 & 9 & 2 6 & 0 & 5 end{pmatrix}.$

Bir matrisdeki düz yatay sıraya satır dikey sıraya sütun adı verilir. Bir matris içinde dizilip gösterilen sayal sayılar öğe veya eleman olarak adlandırılır. Matrisin büyüklüğü satır sayısı ile sutun sayısı birlikte verilmesi ile ifade edilir. Örnek olan verilen matrisler 4x3 (yani 4 satırlı 3 sütunlu) matrislerdir. Matrisin boyutu satır sayısı ve sütun sayısının ayrı ayrı verilmesi ile ifade edilir. Örnek matrislerin boyutu 4 ve 3 olur.

Genel matematiksel notasyon olarak bir matris bir büyük harf ile ifade edilir. Bazan matrislerin daha açık olarak ifadesi notasyonda kullanılan büyük harf vurgulanması ile yapılır. Bu vurgu bilgisayar ile yazılırsa tipografik kalın harf vurgusu ile; elle yazısı ile matris harfinin altına bir (bazan iki) çizgi veya küçük dalgalı bir cizgi koymak suretiyle yapılır. Daha acik bir sekilde notasyon matrisin parantez icinde küçük harfle ifade edilen genel elemanı için i satır ve j sütun alt indisli ve parantez disinda matris buyuklugu verilerek ifade edilir. Örneğin m satırlı n sütunlu mxn türünden bir A matrisi

A veya
$underline{underline{A}}$ veya
$A=[a_{ij}]_{mxn}$

olarak notasyonla ifade edilir.

Böylece genel olarak m ve n pozitif tamsayılar, $i in {1,2,3,4, cdots,m}$ ve $j in {1,2,3,4, cdots,n}$ olmak üzere $a_{i,j}$ sayma sayılarından oluşan yukarıdaki sayılar tablosu matris (dizey) olur. m, matrisin satır sayısını; n ise matrisin sütun sayısını belirtir. m satır ve n sütundan oluşan matrise $mxn$ türünden matris denir:

$mathbf A = A_{m,n} = begin{bmatrix} a_{1,1} & a_{1,2} & cdots & a_{1,n} a_{2,1} & a_{2,2} & cdots & a_{2,n} vdots & vdots & ddots & vdots a_{m,1} & a_{m,2} & cdots & a_{m,n} end{bmatrix}$

Türleri

Kare matris

Satır sayısı sütun sayısına eşit olan matrislerdir.
$A_{2,2} = begin{bmatrix} 2 & -1 0 & 5 end{bmatrix}$
A dizeyi 2x2 türünden bir kare matrisdir.

Birim matris

Kare matrislerin yaygın bir örneği ise, köşegenin üzerindeki öğelerinin 1 geri kalan yerlerdeki öğelerin 0 olduğu birim matristir. Satır ve sütun sayısı n olan bir birim matrisi göstermek için (başka bir yerde kullanılmamışsa) genelde I_n kullanılır. Mesela, 3x3'lük bir birim matris

$I_{3} = begin{bmatrix} 1 & 0 & 0 0 & 1 & 0 0 & 0 & 1 end{bmatrix}$

şeklinde gösterilir.

Sıfır matris

Tüm elemanları sıfır olan matrisdir.
$A_{2,3} = begin{bmatrix} 0 & 0 & 0 0 & 0 & 0 end{bmatrix}$
A dizeyi 2x3 türünden bir sıfır matrisdir.

Satır ve sütun matris

Sadece bir satırdan oluşan matrislere satır, sadece bir sütundan oluşan matrislere ise sütun matris denir.
$A_{m,n} = begin{bmatrix} 0 & 0 & 0 end{bmatrix}$

$B_{m,n} = begin{bmatrix} 0 0 0 end{bmatrix}$

Eğer bir matrisin boyutlarından biri 1 ise (yani ya satır sayısı 1 veya sütun sayısı 1 ise yani satır matrisi veya sütun matrisi ise) bu matris, bir yöney veya vektör veya Euclid-tipi vektör olarak da tanımlanır.

Cebirsel işlemler

Matematikte çarpma ile çarpım farklı kavramlardır. Çarpma bir ikili işlemdir üstelik kapalıdır. Çarpım ise bir daha genel olarak bir göndermedir. Aynı şekilde toplama ile toplam karıştırılmamalıdır.

Matris toplaması

Matrisler bileşenleri karşılıklı olarak toplanırlar.

İki matrisin toplanabilmesi için satır ve sütün sayılarının eşit olması gerekir.

$mathbf{C} = mathbf{A} + mathbf{B} implies c_{ij} = a_{ij} + b_{ij}$

Örnek:

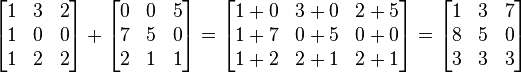
$begin{bmatrix} 1 & 3 & 2 1 & 0 & 0 1 & 2 & 2 end{bmatrix} + begin{bmatrix} 0 & 0 & 5 7 & 5 & 0 2 & 1 & 1 end{bmatrix} = begin{bmatrix} 1+0 & 3+0 & 2+5 1+7 & 0+5 & 0+0 1+2 & 2+1 & 2+1 end{bmatrix} = begin{bmatrix} 1 & 3 & 7 8 & 5 & 0 3 & 3 & 3 end{bmatrix}$

Sayıyla (Skalerle) çarpma

Bir matris, bir sayıyla çarpılırsa her bileşeni o sayıyla çarpılır.

$c_{ij}=k a_{ij}$

Örnek:

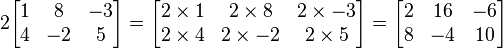
$2 begin{bmatrix} 1 & 8 & -3 4 & -2 & 5 end{bmatrix} = begin{bmatrix} 2times 1 & 2times 8 & 2times -3 2times 4 & 2times -2 & 2times 5 end{bmatrix} = begin{bmatrix} 2 & 16 & -6 8 & -4 & 10 end{bmatrix}$

Matris çarpımı

Matris çarpımı ancak özel bir halde mümkündür ve genelde herhangi iki matris için matris çarpımı işlemi yapılamaz.

Çarpımı istenen iki matris için ilk defa ön-çarpan matris ile art-çarpan matris belirlenmesi gerekir.Çünkü çarpma işlemi sayılarda değişmelidir, fakat matrislerde değildir.Yani genel olarak A ve B matrisi için

AB ≠ BA

AB matris çarpımı için A ön-çarpan ve B art-çarpan; BA matris çarpımı için B ön-çarpan ve A art-çarpan olur. İki matris çarpımı notasyonla belirtilmekle beraber ya AB ya BA ya da hem AB hem BA geçerli olmayabilir.

Matris çarpımı için yapılacak ilk işlem iki matrisin şu kurala uyup uymadığını kontrol etmektir:

Matris çarpımı ancak ön-çarpan sütun sayısı ile art-çarpan satır sayısı birbirine eşitlerse mümkündür.

Yani (pxj) boyutlu A matrisi ile (kxl) boyutlu B matrisinin matris çarpımı AB ancak j=k ise mümkün olur; yoksa geçerli değildir. Bir ek kurala göre de

Eğer matris çarpımı geçerli ise, ortaya çıkartılacak çarpım matrisi ön-çarpan satır sayısı ve art-çarpan matris sütun sayısı boyutludur

Yani eğer j=k ise, matris çarpımı sonucu AB' matrisi (pxl) boyutludur.

Daha sayısal bir örnek olarak A matrisi (2x3) boyutlu ise ve B (3x4) boyutlu ise AB matris çarpımı 3=3 olduğu için geçerlidir ve matris çarpımı işlemi sonuç AB matrisi (2x4) boyutludur. Ama BA matris çarpımı işlemi geçerli değildir, çünkü 4≠2.

A ve B matrislerinin matris çarpımı AB ifadesinin bir şema ile gösterimi.

Matris çarpımının algoritması ilk öğenin i. satırı, ikinci öğenin j. sütunuyla bileşenleri karşılıklı olarak çarpılıp toplanır ve sonuç dizeyin bileşeni olarak yazılır.

A, mxn boyutlu B de nxs boyutlu dizeyler olmak üzere mxs boyutlu sonuç dizey

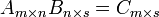
$A_{m times n}B_{n times s} = C_{m times s}$

olarak tanımlanır ve her öğesi

$c_{ij}=sum_{k=1}^{n} a_{ik} b_{kj}$

ile bulunur.

Örnekler

$begin{bmatrix} 1 & 0 & 2 -1 & 3 & 1 end{bmatrix} begin{bmatrix} 3 & 1 2 & 1 1 & 0 end{bmatrix} = begin{bmatrix} (1 times 3 + 0 times 2 + 2 times 1) & (1 times 1 + 0 times 1 + 2 times 0) (-1 times 3 + 3 times 2 + 1 times 1) & (-1 times 1 + 3 times 1 + 1 times 0) end{bmatrix} = begin{bmatrix} 5 & 1 4 & 2 end{bmatrix}$

Çarpmayı, ilk öğenin her satırını bir yöney ve ikinci öğenin her sütununu bir yöney olarak düşünüp ilk öğeyi bir sütun yöney ve ikinci öğeyi bir satır yöney olarak yöney iç çarpımına indirgeyebiliriz. Örneğin, $vec{a}$ ve $vec{b}$ yöneyleri n boyutlu olmak üzere,

$A_{m times n}=begin{bmatrix} vec{a_1} cdots vec{a_m} end{bmatrix}$ ve $B_{n times s}=begin{bmatrix} vec{b_1} && cdots && vec{b_s} end{bmatrix}$

şeklinde düşünüldüğünde çarpım,

$A B = begin{bmatrix} vec{a_1} cdot vec{b_1} && cdots && vec{a_1}cdotvec{b_s} vdots && ddots && ddots vec{a_m}cdotvec{b_1} && cdots && vec{a_m}cdotvec{b_s} end{bmatrix}$

biçimini alır. Bu şekilde düşünmek kâğıt üzerinde dizeyleri çarparken işe yarayabilir ve zaman kazandırır.

$begin{bmatrix} 3 & 0 -1 & 2 end{bmatrix} begin{bmatrix} 7 & -1 3 & 6 end{bmatrix}$	$= begin{bmatrix} (3,0) (-1,2) end{bmatrix} begin{bmatrix} (7,3) & (-1,6) end{bmatrix}$
	$= begin{bmatrix} (3,0)cdot(7,3) && (3,0)cdot(-1,6) (-1,2)cdot(7,3) && (-1,2)cdot(-1,6) end{bmatrix}= begin{bmatrix} 21 && -3 -1 && 13 end{bmatrix}$

Kronecker (Doğrudan) toplam

Bu toplamın sonucu bir matrisler köşegenidir.

$C=oplus_{i=1}^{k} A_i=text{kosegen}left( A_1,A_2,...,A_k right)=left[ begin{array}{cccc} A_1 & 0 & cdots & 0 0 & A_2 & cdots & 0 vdots & vdots & ddots & vdots 0 & 0 & cdots & A_k end{array} right]$

burada sonuç dizeyin boyutları, toplanan dizeylerin doğrudan boyutları toplamı kadardır.

Kronecker (Doğrudan) çarpım

Bu çarpım ilk öğenin her bileşenini ikinci öğeyle doğrudan çarpmayla tanımlanır.

$A_{m times n} otimes B_{r times s} = left[ begin{array}{cccc} a_{11}B & a_{12}B & cdots & a_{1n}B a_{21}B & a_{22}B & cdots & a_{2n}B vdots & vdots & ddots & vdots a_{m1}B & a_{m2}B & cdots & a_{mn}B end{array} right]$

buradan,

$C_{(m r) times (n s)}=left[ begin{array}{ccccc} a_{11}b_{11} & a_{11}b_{12} & cdots & a_{12}b_{11} & cdots a_{11}b_{21} & a_{11}b_{22} & cdots & a_{12}b_{21} & cdots vdots & vdots & ddots & quad & quad a_{21}b_{11} & a_{21}b_{12} & quad & ddots & quad vdots & vdots & quad & quad & ddots end{array} right]$

Cebirsel ifade bir ya da birden fazla cebirsel terimin aynı ifade de yer almasına denir. Örneğin x sayısı gibi. Cebirsel ifadelerde en çok kullanılanlar: x,y,n dir. Cebirsel ifadelerle kurulmuş iki eşitliğe denklem denir. Mesela x+5=2x+2 çözüm bilenenler bir tarafa bilinmeyenler bir tarafa gönderilir. Öteki tarafa geçerken zıt işaret verilir yani: +5-2=2x-x sadeleştirirsek 3=x

Doğrusal denklemler sistemleri

Örnek olarak dört bilinmeyenli (x₁, x₂, x₃ ve x₄) dört tane doğrusal denklemler sistemi ele alınsın. Bu denklemlerdeki katsayılar, i denklem sayısı, j bilinmeyen olursa, a_i,j olarak ifade edilebilir. Bu halde doğrusal denklemler sistemi şöyle yazılır:

$begin{align} a_{11} x_1 + a_{12} x_2 + a_{13} x_3 + a_{14} x_4 &= b_1 a_{21} x_1 + a_{22} x_2 + a_{23} x_3 + a_{24} x_4 &= b_2 a_{31} x_1 + a_{32} x_2 + a_{33} x_3 + a_{34} x_4 &= b_3 a_{41} x_1 + a_{42} x_2 + a_{43} x_3 + a_{44} x_4 &= b_4 end{align} ~.$

Bu denklemler sistemi matris kullanılarak çok basit bir şekle indirilebilir. Matrislerle sistem şöyle ifade edilir:

$begin{bmatrix} a_{11} & a_{12} & a_{13} & a_{14} a_{21} & a_{22} & a_{23} & a_{24} a_{31} & a_{32} & a_{33} & a_{34} a_{41} & a_{42} & a_{43} & a_{44} end{bmatrix} begin{bmatrix} x_1 x_2 x_3 x_4 end{bmatrix} = begin{bmatrix} b_1 b_2 b_3 b_4 end{bmatrix} ~.$

Daha kısa bir notasyonla bu şöyle yazılabilir:

$left[mathsf{A}right] left[mathsf{x}right] = left[mathsf{b}right] ~~~~text{or}~~~~ mathbf{A} mathbf{x} = mathbf{b} ~.$

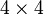Burada $mathbf{A}$ $4times 4$ boyutlu matrisdir; $mathbf{x}$ ve $mathbf{b}$ $4times 1$ boyutlu sutun matrislerdir.

Genel olarak n sayıda değişkenli m sayıda doğrusal denklemden oluşan şu doğrusal denklemler sistemi:

A_1,1x₁ + A_1,2x₂ + ... + A_1,nx_n = b₁

...

A_m,1x₁ + A_m,2x₂ + ... + A_m,nx_n = b_m

çok kolayca bir denklemler matrisi olarak ifade edilebilir. Bunun için x yöneyi n değişken ('x₁, x₂, ..., x_n) için bir n-sütun yöneyi (yani 'n×1-matrisi); A matrisi mxn boyutlu katsayılar matrisi ve b n-sutun yöneyi halindeki denklem sabitleri olursa, herhangi bir doğrusal denklem sistemi matris denklemi olarak şöyle ifade edilir:

Ax = b.

Matematiksel matris kavramının tarihsel kaynağı

Doğrusal denklemler sistemlerinin çözülmesi için matris kavramlarının kullanılmasının çok uzun bir tarihi bulunmaktadir. Doğrusal denklemler sistemlerin ilk matris kullanarak açıklanıp çözülmesi, özellikle kare matrislerle ifade edilip determinant kullanımı dahil, MO.300 ile MS.200 arasında yazılmış olan Jiu Zhang Suan Shu (Matematik Sanatinda Dokuz Bolum) adli eserde bulundugu anlaşılmıştır. Bu eserden Batı Avrupa matematikçileri hiç haberdar olmamışlardır. Bundan sonra matris kavramı 2000 yıl kadar sonra 1683de "Seki Kowa" adlı Japon matematikçisi ve Batı Avrupa'da ilk defa 1693de Alman matematikçisi Leibniz tarafından ortaya atılmış ve ilk determinant kullanarak pratik çözüm olarak Cramer'in kuralı 1750'de Gabriel Cramer tarafından gösterilmiştir.

Matris teorisinin Batı Avrupa'da geliştirilmesi daha çok determinant kavramına önem vermekteydi. Determinantdan bağımsız olarak matris matematiğinin geliştirilmesi 1858de Arthur Cayley tarafından Memoir on the theory of matrices (Matris teorisi hakkında bir not) adında eserle başlamıştır. Matris terimi isim olarak ilk defa J.J.Syvester adlı İngiliz matematikçisi tarafından kullanılmıştır. Bu matematikçi determinantları açıp sayısal değerlerini bulmak için sutun ve satırları silip gittikçe daha küçük determinant (minor) elde ederek bu sonuca bulma üzerinde uğraşı göstermiş ve sanki bir ana determinantan gittikçe küçülen "çocuk" determinantların bulunmasından ilham alarak simdi matris olarak adlandırdığımız kavrama Latince kökten mater (anne) sözcüğünden çıkardığı matrix adını vermiştir.